ARTICOLO DOPPIO.
Dopo aver compreso i concetti preliminari di Punto di Accumulazione e di Punto Isolato siamo finalmente pronti per acquisire anche la definizione teorica di limite.
Si distinguono quattro casi:
LIMITE FINITO PER x TENDENTE A UN VALORE FINITO
Limite Finito per x Tendente a un Valore Infinito
Limite Infinito per x Tendente a un Valore Finito
Limite Infinito per x Tendente a un Valore Infinito
Il caso di cui si parla in questa lezione è quello in cui si calcola un limite per x tendente a un valore finito di una funzione reale di variabile reale, ottenendo un valore reale (cioè un numero e quindi un valore finito).
Il tipo di limite che stiamo ora trattando, in particolare, ci permetterà di dire come si comporta una funzione in prossimità dei punti che sono esclusi dal dominio, come ad esempio nel caso di una funzione y=f(x) con dominio del tipo [a;x0[u]x0;b]. Ci si chiede: quanto vale f(x0)? Per saperlo si calcolo il limite infinito per x tendente ad un valore finito, puoi sapere come si comporta la funzione nell’intorno di quel punto.
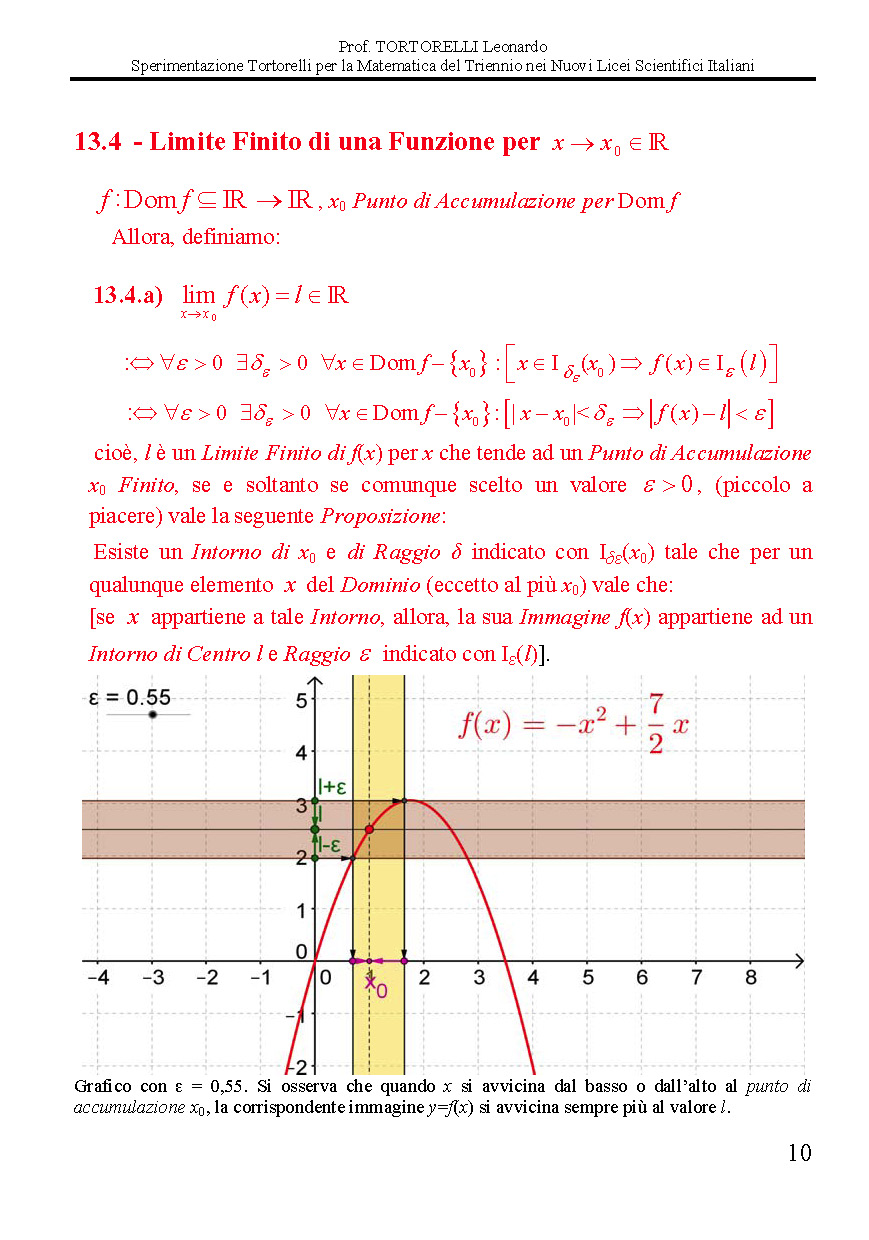
DEFINIZIONE DI LIMITE FINITO PER X TENDENTE AD UN VALORE FINITO
In coda all’articolo troverete l’ormai tradizionale area download dove potrete scaricare un meraviglioso pdf da visualizzare sul vostro pc, tablet o smartphone.
– – – – – – – – – – – – – – – – – – – – – – – –
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – –